今天的內容會比較偏向理論的部分，因此會比較無趣，但量子糾錯的原理是基於這個成立的，因此很重要。

Error-correcting codes

為了定義糾錯碼(error correcting code)，我需要以下三件事:

1. The dimension of the message space, k.
2. The dimension of the codespace, n.
3. The code C
   糾錯碼通常標記為 [ 𝑛 、𝑘 、𝑑 ] ，其中距離 𝑑是稍後將定義的東西。這是一種不規範的情況，因為可能有多個具有相同的程式碼 𝑛 , 𝑘 , 𝑑 但不同 C。然而，這些參數在上下文中通常足以識別代碼。

編碼過程

上面給出的程式碼的定義是相當抽象的。為了對訊息進行編碼和解碼損壞的碼字，我們需要一個更具體的定義來給出明確的計算過程。這是透過給出明確的定義來完成的C

對於任何程式碼，我們都可以確定一個基本集合C。例如，對於重複碼(repetition code)，基本組合為(111)

我們現在將向量寫為行矩陣而不是位元字串。一般來說，會有 𝑘 這樣的向量，因為子空間是 𝑘
維，每個向量的長度 𝑛 。我們可以收集這些 𝑘 將向量轉換為矩陣的行，稱為生成矩陣。

生成矩陣 𝐺 , 是一個 𝑘×𝑛 其行是程式碼基礎的矩陣 𝐂

對於重複碼，生成矩陣是𝐺 = (111).
任何留言 𝐦 可以編碼成碼字 𝐜 使用生成矩陣。程式碼的碼字都在其生成矩陣的行空間中 𝐺 ，即碼字集合是{ 𝑐 = 𝐦 𝐺 : 𝐦 ε }

程式碼完全使用生成矩陣來指定。
因為程式碼的基礎 𝐶 不是唯一的，同一程式碼可以有許多可能的生成矩陣 𝐶
我們可以透過對生成矩陣進行行操作來在不同的程式碼之間進行轉換，這不會改變行空間。在生成矩陣的形式中，有一個標準形式，即𝐺 = [| 𝐴]
， 是個𝑘×𝑘單位矩陣和𝐴是一個𝑘 × ( 𝑛 − 𝑘 )矩陣

漢明碼(Hamming code)

重複程式碼(repetition code)是一個非常簡單的程式碼。為了理解更多關於糾錯的概念，我們需要更複雜的程式碼。漢明碼就是為了這個目的。它是一個 [7,4,3] 代碼，表示長度的消息 4 被編碼成長度的碼字 7
為了定義漢明碼，我們需要定義 𝐂 。首先我們定義如何建構 𝐜 從一個 𝐦 。前四位 𝐜 實際上是一樣的 𝐦
𝑐1𝑐2𝑐3𝑐4=𝑚1𝑚2𝑚3𝑚4
剩下的位， 𝑐5𝑐6𝑐7 透過使用奇偶校驗的概念來定義。

位元串的奇偶校驗是根據其中 1 的數量計算的。如果 1 的個數為偶數，則該字串的奇偶校驗為偶數或 0，否則為奇數或 1。
例如，奇偶校驗 101 是 0 並且 01011 是 1。

對於漢明碼，我們計算訊息位元的各個子集的奇偶校驗，並將它們儲存在碼字中。如果代碼字被損壞，一些奇偶校驗會發生變化，這使我們能夠識別錯誤。有四個消息位。有 4𝐶3=4 大小為三的子集。我們計算其中三個子集的奇偶校驗。從下圖中可以很容易地看出這一點。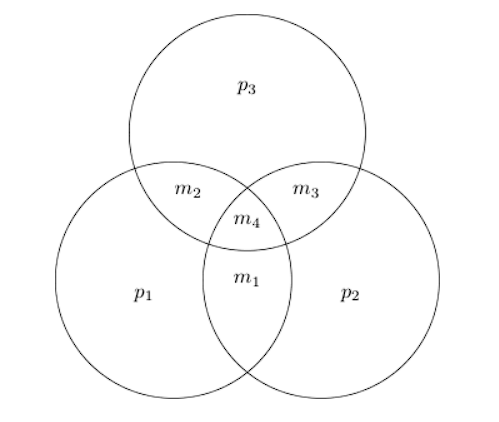

• 𝑝1是𝑚1,𝑚2,𝑚4的奇偶性
• 𝑝2是𝑚1,𝑚3,𝑚4的奇偶性
• 𝑝3是𝑚2,𝑚3,𝑚4的奇偶性

第四子集的奇偶校驗（ 𝑚1,𝑚2,𝑚3 ) 取決於其他三個的奇偶性，因此不需要計算。完整的碼字是𝐜 = (𝑚1 𝑚2 𝑚3 𝑚4 𝑝1 𝑝2 𝑝3).

在我們深入研究數學之前，讓我們先討論一下該協議是如何運作的。Alice 根據上面的規定建立碼字並將其發送給 Bob。當鮑伯收到損壞的碼字時，他計算前四位的三個奇偶校驗（ 𝐜̃ 1,𝐜̃ 2,𝐜̃ 3,𝐜̃ 4) 並將它們與損壞的碼字的最後三位進行比較（ 𝐜̃ 5,𝐜̃ 6,𝐜̃ 7 ）。如果某些奇偶校驗不同，則表示發生了錯誤。

假設錯誤發生在 𝐜1 。從圖中我們可以看出，這意味著 𝑝1 和 𝑝2 將會被翻轉。另一方面，錯誤 𝐜2 將導致 𝑝1 和 𝑝3 被翻轉。類似地，如果錯誤發生在奇偶校驗位上，則只有該奇偶校驗位會被翻轉。因此，單一奇偶校驗位不同表示其上有錯誤，而兩個或三個奇偶校驗位差異則表示「訊息位」上有錯誤。

參考資料:https://github.com/abdullahkhalids/qecft